
1. 신경망의 정의
- 인공신경망(Artificial Neural Network), 다층 퍼셉트론
- 입력층과 출력층 사이에 은닉층이 존재
- 여러층으로 구성되고 시그모이드 함수 등 매끈한 활성화 함수를 사용하는 네트워크
2. 신경망의 구조

- 입력층(input layer), 은닉층(hidden layer), 출력층(output layer)
- 입력층 : 주어진 데이터가 입력되는 층으로서, 일반적으로 스칼라 또는 벡터의 형태로 입력됨.
- 출력층 : 입력층과 은닉층을 거쳐 형성된 최종 데이터를 갖는 층. 해당 데이터를 바탕으로 설정된 작업을 수행.
- 은닉층 : 은닉층의 뉴런은 사람 눈에 보이지 않는다.
- 위 그림은 가중치를 갖는 층이 2개이므로 '2층 신경망'이라고 부른다.
- 보통 은닉층이 1개 일때 '얕은 신경망'이라고 하며, 5개 이상일때 '심층 신경망(DNN)'이라고 부른다.
출력 = weight(가중치) * 입력값 + bias
Y = 0 W1*X1 + W2*X2 <= - bias
Y = 1 W1*X1 + W2*X2 > - bias
Y = 0 W1*X1 + W2*X2 + bias <= 0
Y = 1 W1*X1 + W2*X2 + bias > 0
|
weight |
|
| # 파이썬 코드로 구현 x = np.array([0,1]) |
 |
편향(bias)이 필요한 이유?
편향이 없다면 무조건 원점을 지나는 직선의 방정식이 나오기 때문에
신경망 구현
1. 행렬의 곱
1) 1차원 배열 만들기
| # numpy 라이브러리 불러오기 import numpy as np |
|
|
# 1차원 배열 만들기 a = np.array([1,2,3,4]) |
 |
|
# 차원의 수 확인 np.ndim(a) |
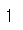 |
|
# 배열의 모양 확인 a.shape |
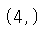 |
2) 2차원 배열의 곱
|
# 2차원 배열 만들기 a = np.array([[1,2],[3,4]]) b = np.array([[5,6],[7,8]]) |
 |
|
# 차원의 수 확인 np.ndim(a) np.ndim(b) |
 |
|
# 배열의 모양 확인 a.shape b.shape |
 |
|
# 행렬의 곱 (내적) / 2x2 * 2x2 = 2x2 np.dot(a,b) |
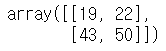 |
|
# 2차원 배열 만들기 a = np.array([[1,2,3],[4,5,6]]) b = np.array([[1,2],[3,4],[5,6]]) |
 |
|
# 차원의 수 확인 np.ndim(a) np.ndim(b) |
 |
|
# 배열의 모양 확인 a.shape b.shape |
 |
|
# 행렬의 곱(내적) / 2x3 * 3x2 = 2x2 np.dot(a,b) |
 |
|
# 2차원 배열 만들기 a = np.array([[1,2],[3,4],[5,6]]) b = np.array([7,8]) |
 |
|
# 차원의 수 확인 np.ndim(a) np.ndim(b) |
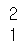 |
|
# 배열의 모양 확인 a.shape b.shape |
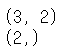 |
|
# 행렬의 곱(내적) / 3x2 * 2 = 3 np.dot(a,b) |
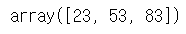 |
|
# 2차원 배열 만들기 a = np.array([1,2]) b = np.array([[1,2,3],[4,5,6]]) |
 |
|
# 차원의 수 확인 np.ndim(a) np.ndim(b) |
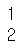 |
|
# 배열의 모양 확인 a.shape b.shape |
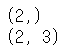 |
|
# 행렬의 곱(내적) / 2 * 2x3 = 3 np.dot(a,b) |
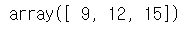 |
2. 3층 신경망 구현
|
# 입력층, 0층 x = np.array([0.1,0.5]) w1 = np.array([[0.1,0.3,0.5],[0.2,0.4,0.6]]) b1 = np.array([0.1,0.2,0.3]) x.shape w1.shape b1.shape |
 |
|
# 첫번째 은닉층, 1층 a1 = np.dot(x,w1) + b1 # 활성화 함수 사용 (시그모이드) def sigmoid(x) : return 1/(1+np.exp(-x)) z1 = sigmoid(a1) z1 |
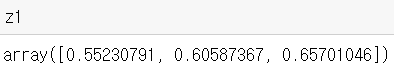 |
|
# 두번째 은닉층, 2층, 2개 뉴런 w2 = np.array([[0.1,0.4],[0.2,0.5],[0.3,0.6]]) b2 = np.array([0.1,0.2]) a2 = np.dot(z1,w2) + b2 z2 = sigmoid(a2) z2 |
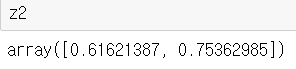 |
|
# 출력층 3층, 2개 뉴런 w3 = np.array([[0.1,0.3],[0.2,0.4]]) b3 = np.array([0.1,0.2]) a3 = np.dot(z2,w3) + b3 y = sigmoid(a3) y |
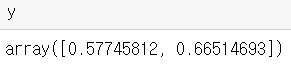 |
'인공지능 > 딥러닝' 카테고리의 다른 글
| 손실 함수(Loss Function)와 최적화(Optimizer) (0) | 2020.04.27 |
|---|---|
| 신경망의 출력층 (0) | 2020.04.21 |
| 활성화 함수 (0) | 2020.04.20 |
| 인공지능 / 머신러닝과 딥러닝의 차이점 (0) | 2020.04.19 |
| 퍼셉트론 (0) | 2020.04.13 |