활성화 함수

 

 

 

1. 활성화 함수(Activation Function)란?

 

https://m.blog.naver.com/worb1605/221187949828

 

 

• synapse는 전달된 전기신호가 최소한의 자극 값을 초과하면 활성화되어 다음 뉴런으로 전기신호를 전달한다.
• 활성화 함수는 이것을 모방하여 값이 작을때는 출력값을 작은겂으로 막고 일정한 값을 초과하면 출력값이 급격히 커지는 함수를 이용한다.
• 신경망에서는 전달받은 데이터를 가중치를 고려해서 합산하고 그 값을 활성화 함수를 적용해 다음층에 전달한다.
• 신경망에서는 활성화 함수로 비선형함수를 사용해야 한다.
• 입력 신호의 총합을 출력신호로 변환하는 함수
• 입력 신호의 총합이 활성화를 일으키는 지를 정하는 역할
• 가중치가 곱해진 입력 신호의 총합을 계산하고, 그 합을 활성화 함수에 입력해 결과를 내는 2단계로 처리된다.
• 입력 신호의 총합 계산 : a = w1x1 + w2x2 + b
  합을 활성화함수에 입력하여 결과 출력 : y = h(a)

 

 

2. 활성화 함수의 종류

https://www.slideshare.net/ssuser892bc4/dl-from-scratch13

 

2-1 계단 함수 (step function)

 

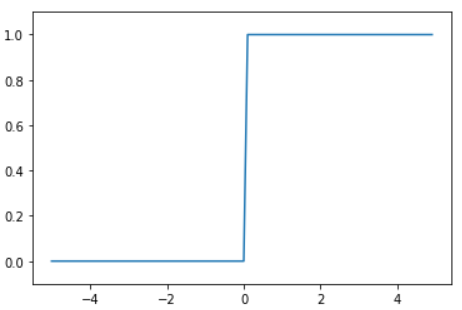
• 계단모양의 함수
• 퍼셉트론에서 사용하는 활성화 함수
• 임계치를 넘으면 출력값이 0 또는 1로 나온다.

 

2-2 시그모이드 함수 (sigmoid function)

 

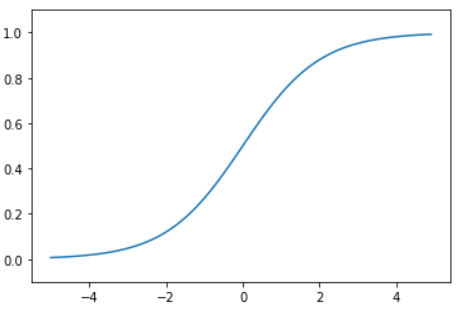
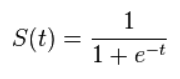
• S자 모양의 함수
• 출력이 0과 1사이의 값만 가질 수 있도록하는 비선형 함수
• 0과 1사이의 연속적인 출력값을 가질 수 있다.
• 입력이 중요하면 큰 값을 출력하고 입력이 중요하지 않으면 작은 값을 출력한다.
• 깊은 신경망을 쌓을 수 있게 만들어 준다.
• 하지만 신경망이 너무 깊어지면 출력이 값이 0이나 1로 수렴하게 되어서 그래디언트를 소멸시켜 버린다.
  (Gradient Vanishing)
• 0이 아니라 0.5가 중심이기 때문에 항상 양수를 출력해서, 출력의 가중치 합이 입력의 가중치 합보다 커질 가능성이 높다.(편향이동)
• 각 레이어를 지날 때마다 분산이 계속 커져 가장 높은 레이어에서느 0이나 1로 수렴하게 되는 문제점이 있다.
• 신경망에서 자주 이용하는 함수

 

 

2-3 렐루함수 (ReLU function)

 

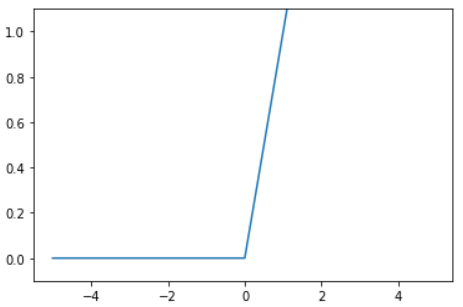
• 직역하면 정류된 선형 함수라는 뜻이다.
• 입력값이 양수이면 그대로 출력하고, 0이하면 0으로 출력한다.
• 시그모이드 함수의 Gradient Vanishing 문제를 해결하기 위해 사용되는 활성화 함수이다.
• 미분이 간단해 진다.

 

 

3. 활성화 함수 구현하기

계단 함수 (step function)
import numpy as np import matplotlib.pylab as plt   def step_function(x) :     return np.array(x > 0, dtype = np.int) x = np.arange(-5.0, 5.0, 0.1) y = step_function(x) plt.plot(x, y) plt.ylim(-0.1, 1.1) plt.show()
시그모이드 함수 (Sigmoid function)
import numpy as np  import matplotlib.pylab as plt   def sigmoid(x):     return 1/(1+np.exp(-x)) x = np.arange(-5.0, 5.0, 0.1) y = sigmoid(x) plt.plot(x, y) plt.ylim(-0.1, 1.1) plt.show()
렐루 함수 (ReLU function)
import numpy as np  import matplotlib.pylab as plt   def relu(x):      return np.maximum(0, x) x = np.arange(-5.0, 5.0, 0.1)  y = relu(x)  plt.plot(x, y)  plt.ylim(-0.1, 1.1)  plt.show()