
1. 손실 함수 (Loss Function)
- 손실 함수는 실제값과 예측값의 차이(loss, cost)를 수치화해주는 함수이다.
- 오차가 클수록 손실 함수의 값이 크고, 오차가 작을수록 손실 함수의 값이 작아진다.
- 손실 함수의 값을 최소화 하는 W, b를 찾아가는것이 학습 목표이다.
- 회귀 : 평균제곱오차 / 분류 : 크로스 엔트로피
1-1 평균 제곱 오차 (Mean Squared Error, MSE)
- 연속형 변수를 예측할 때 사용한다.

|
def MSE(y, t): return (1/2) * np.sum((y-t)**2) |
1-2 크로스 엔트로피 (Cross-Entropy)
- 낮은 확률로 예측해서 맞추거나, 높은 확률로 예측해서 틀리는 경우 loss가 더 크다.
- 이진분류 : binary_crossentropy / 다중분류 : categorical_crossentropy
- y : 실제값(0혹은1) / y^ : 예측값(확률)
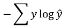
|
def cross_entrpy_error(y, t): delta = le - 7 return -np.sum(t * np.log(y + delta)) |
2. 최적화 (Optimizer, 옵티마이저)

- 손실함수를 줄여나가면서 학습하는 방법은 어떤 optimizer를 사용하느냐에 따라 달라진다.
2-1 경사 하강법(Gradient Descent)

- 가장 기본적인 optimizer 알고리즘
- 경사를 따라 내려가면서 가중치(w) 업데이트 시킨다.
- 손실함수를 최소화하기 위하여 반복적으로 파라미터를 조정해나가는 방법
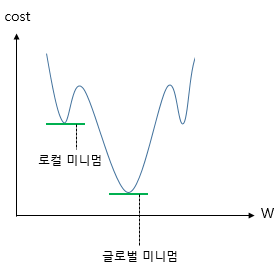
- 학습률(learning rate)이 너무 크면 학습시간이 짧아지나 전역 최솟값에서 멀어질 수 있음
- 학습률(learning rate)이 너무 작으면 학습시간이 오래걸리고 지역 최솟값에 수렴할 수 있음
2-2 배치 경사 하강법(batch Gradient Descent)
- 배치(batch) : 가중치 등의 매개 변수의 값을 조정하기 위해 사용하는 데이터의 양
- 배치를 전체 데이터로 두는것
- 1epoch당 시간은 오래 걸리고 메모리를 크게 요구하나, 전역 최솟값을 찾을 수 있다.
| model.fit(X_train, y_train, batch_size=len(trainX)) |
2-3 확률적 경사 하강법(Stochastic Gradient Descent, SGD)
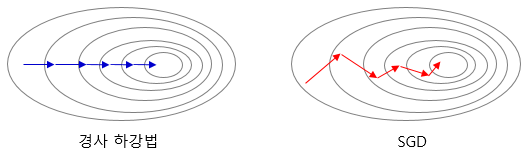
- 매개변수 값을 조정 시 전체 데이터가 아니라 랜덤으로 선택한 하나의 데이터에 대해서만 계산하는 방법
- 더 적은 데이터를 사용하므로 더 빠르게 계산할 수 있다.
- 때로는 배치 경사 하강법 보다 정확도가 낮을 수 있다.
| model.fit(X_train, y_train, batch_size=1) |
2-4 미니 배치 경사 하강법 (Mini-Batch Gradient Descent)
- 정해준 데이터 양에 대해서만 계산한여 매개변수 값을 조정한다.
- 전체 데이터를 계산하는 것보다 빠르며, SGD보다 안정적이다.
- 실제로 가장 많이 사용되는 경사 하강법이다.
| model.fit(X_train, y_train, batch_size=32) #32를 배치 크기로 하였을 경우 |
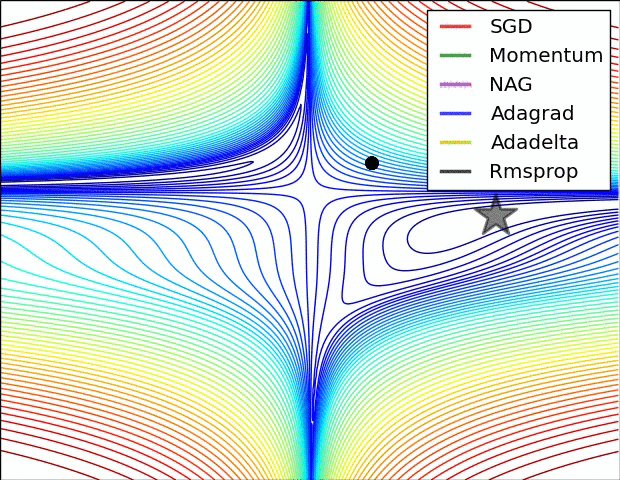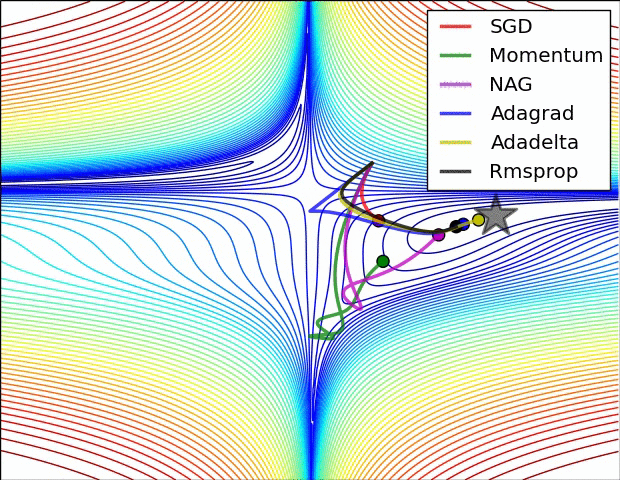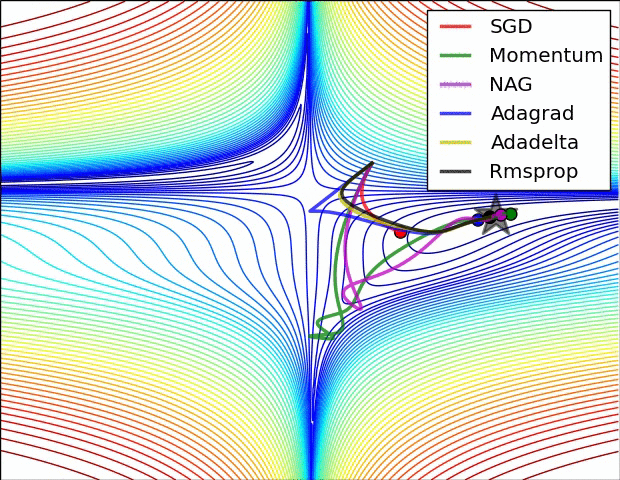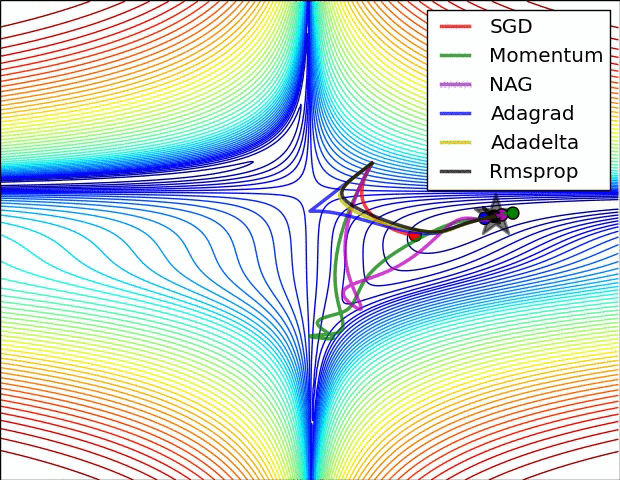
2-5 모멘텀(Momentum)
- 관성이라는 물리학 법칙을 응용한 방법
- 경사 하강법 + 관성
- 계산된 접선의 기울기에 한 시점(step)전의 접선의 기울기 값을 일정한 비율만큼 반영
- 지역 최솟값에 빠지더라도 관성의 힘으로 빠져나올 수 있다.
2-6 아담(Adam)
- RMSprop와 모멘텀을 합친 방법
- 방향과 학습률 두 가지를 모두 잡기 위한 방법
| keras.optimizers.Adam(lr=0.001, beta_1=0.9, beta_2=0.999, epsilon=None, decay=0.0, amsgrad=False) |


반응형
'인공지능 > 딥러닝' 카테고리의 다른 글
| 딥러닝의 종류와 개념 (0) | 2020.05.05 |
|---|---|
| 데이터 학습 과정 정리 (2) | 2020.04.27 |
| 신경망의 출력층 (0) | 2020.04.21 |
| 활성화 함수 (0) | 2020.04.20 |
| 인공지능 / 머신러닝과 딥러닝의 차이점 (0) | 2020.04.19 |