
의사결정트리
- 지도학습
- 해석력이 좋다.(현장에서 많이쓰임) : 어떤컬럼을 먼저 바라봐야 분류가 잘되는지
- 의사결정규칙(decision rule)을 나무구조(tree)로 도표화하여 분류와 예측을 수행하는 분석방법이다.
활용분야
- 은행대출 : 도산업체 분류 (예측) 과거의 데이터로부터 도산기업과 도산화지 않은 기업을 찾아내는 방법
- 카드 발급 대상 : 신용불량자 분류 (예측)
- 통신 : 이탈고객 (해지자, 번호이동) 분류, 새로운 서비스 대상 고객선정
- 쇼핑 : direct mailing 대상 고객선정
장점
- 지도학습 (분류, 예측)의 데이터마이닝 기법
- 규칙의 이해가 쉽다, SQL과 같은 DB언어로 표현
- 적용결과에 의해 IF-THEN 으로 표현되는 규칙이 생성
- 해석력이 좋다.
분류알고리즘(R)
- C5.0 : 엔트로피 지수(entropy index)
C5.0은 엔트로피와 정보이득(imformation gain)
목표변수의 데이터들이 혼재되어 있으면 무질서도 즉 엔트로피가 큰 상태가 되는데 입력변수들의 데이터들을 여러 그룹으로 나누는 과정에서 목표변수의 엔트로피를 낮추는 방향으로 진행된다.
이때 목표 변수는 정보이득이 발생하게 되는데 그 값을 가장 크게 해주는 입력변수를 우선적으로 의사결정나무 상위계층으로 분류한다. (정답을 찾기위해 제일먼저 물어봐야할 컬럼 찾기)
엔트로피와 정보이득 구하기
# 데이터 불러오기
read.csv("C:/data/titanic2020.csv")

목표변수 : 생존여부 (Y-생존 / N-사망)
분류를 잘하기 위해 엔트로피값이 가장 높은컬럼을 찾자
# 생존여부 엔트로피 구하기
H(생존여부) 엔트로피 (∑-Plog2(P)):
P(생존) = 7/10
P(사망) = 3/10
= - P(생존)log2P(생존) - P(사망)log2P(사망)
= -7/10 * log2(7/10) - 3/10 * log2(3/10)
= 0.8812
엔트로피 구하기
| 좌석등급에 대한 엔트로피 구하기 | |
| 1등급일때 생존여부 구하기 |
H(생존여부|1) 엔트로피 (∑-Plog2(P)) P(생존|1) = 4/4 P(사망|1) = 0/4 = - P(생존)log2P(생존) - P(사망)log2P(사망) = -4/4 * log2(4/4) - 0/4 * log2(0/4) = 0 |
| 2등급일때 생존여부 구하기 |
H(생존여부|2) 엔트로피 (∑-Plog2(P)): P(생존|2) = 3/6 P(사망|2) = 3/6 = - P(생존|2)log2P(생존|2) - P(사망|2)log2P(사망|2) = -3/6 * log2(3/6) - 3/6 * log2(3/6) = 1 |
| 등급에 따른 생존여부 구하기 |
H(생존여부|좌석등급) 엔트로피 (∑-Plog2(P)): P(1)*P(생존여부|1) + P(2)*P(생존여부|2) = 4/10*0 + 6/10*1 = 0.6 |
| 성별에 대한 엔트로피 구하기 | |
| 남성일때 생존여부 구하기 |
H(생존여부|M) 엔트로피 (∑-Plog2(P)) P(생존|M) = 4/7 P(사망|M) = 3/7 = -4/7*log2(4/7) -3/7*log2(3/7) = 0.98 |
| 여성일때 생존여부 구하기 |
H(생존여부|F) 엔트로피 (∑-Plog2(P)) P(생존|F) = 3/3 P(사망|F) = 0/3 = -3/3*log2(3/3) - 0/3*log2( 0/3) = 0 |
| 성별에 따른 생존여부 구하기 |
H(생존여부|성별) 엔트로피 (∑-Plog2(P)): P(M)*P(생존여부|M) + P(F)*P(생존여부|F) = 7/10*0.98 + 3/10*0 = 0.68 |
정보이득 구하기
이전 엔트로피 - 이후 엔트로피
| 좌석등급의 정보이득 |
iq(생존여부, 좌석등급) = H(생존여부) - H(생존여부|좌석등급) = 0.88 - 0.6 = 0.28 |
| 성별의 정보이득 |
iq(생존여부, 성별) = H(생존여부) - H(생존여부|좌석등급) = 0.88 - 0.686 = 0.194 |
!!! 정리 !!!
|
엔트로피값이 높으면 분류가 잘 되어있는것 |
|
데이터의 엔트로피 : 데이터가 무질서하면 엔트로피가 높음 / 질서가 있으면 엔트로피가 낮음 데이터의 엔트로피로 컬럼의 엔트로피를 구함 컬럼의 엔트로피 : 무질서하면 엔트로피가 높음 / 질서가 있으면 엔트로피가 낮음
컬럼의 엔트로피로 정보이득 구함 정보이득 : 컬럼의 엔트로피가 높으면 정보이득이 낮음 / 컬럼의 엔트로피가 낮으면 정보이득이 높음
즉, 데이터,컬럼이 무질서하면 엔트로피값이 높고 정보이득이 낮음 (성별) 데이터,컬럼이 질서하면 엔트로피값이 낮고 정보이득이 높음 (좌석등급)
|
의사결정트리의 노드
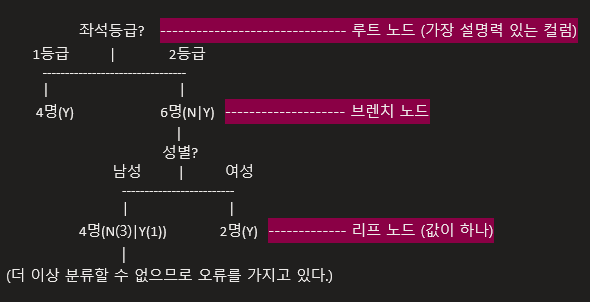
정지 규칙:
정지규칙은 더 이상 분리가 일어나지 않고 현재의 마디가 끝마디가 되도록하는 규칙이며 가지치기는 형성된 의사결정나무에서 적절하지 않은 마디를 제거하여 적당한 크기의 부나무(Subtree)구조를가지는 의사결정나무를 최종적인 예측모형으로 선택하는 것이다.
오버피팅 :
- 너무 노드가 깊어지면 오분류의 가능성이 생긴다.
- 훈련 데이터셋은 잘 분류하나 테스트 데이터셋은 잘 분류하지 못함
- 중간중간 노드를 절단할 필요가 있음
오버피팅을 줄이는 방법 :
- 데이터 많이 사용하기
- 중간 노드들을 없애기
의사결정트리 구현 (R)
|
# 라이브러리 설치 install.packages("C50") library(C50) |
|
|
# 목표변수~., data = 사용컬럼 C5.0(생존여부~.,data=titanic) |
 |
|
# summary 확인 model <- C5.0(생존여부~.,data=titanic[,-1]) summary(model) |
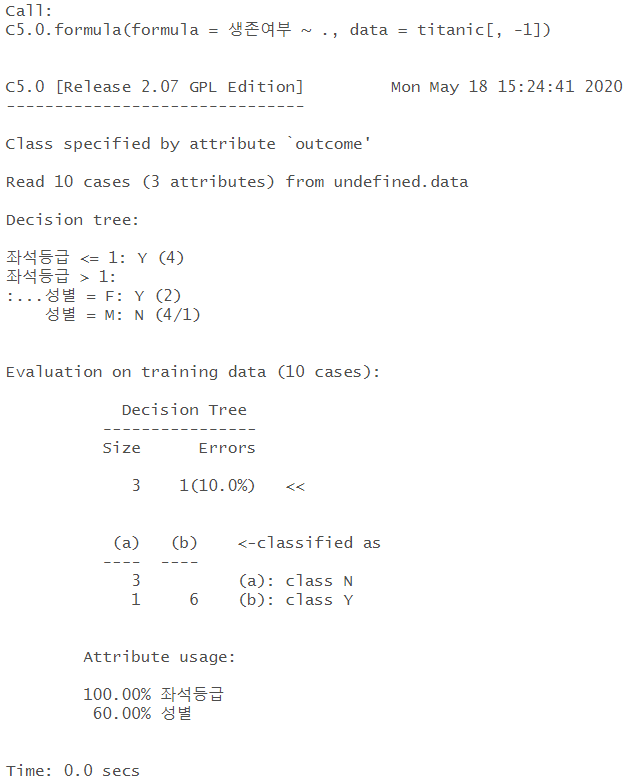 |
| < summary 해석1 > 1개가 에러남 |
 |
| < summary 해석2 > 4개가 N으로 분류되어야 하지만 1개가 오분류가 됨. |
 |
| < summary 해석3 > 어떤 컬럼이 설명력 있는지 확인할 수 있음 |
 |
|
# 특정한 열만 사용 model <- C5.0(생존여부~좌석등급+성별,data=titanic[,-1]) summary(model) |
 |
|
# 그림으로 그리기 plot(model) |
 |
|
# 예측하기 : 한번도 경험하지 않은것도 분류 가능 test_data = data.frame("좌석등급"=3, "성별"="F") predict(object=model,newdata = test_data) |
 |
'인공지능 > 머신러닝' 카테고리의 다른 글
| 의사결정트리 시각화 (0) | 2020.05.23 |
|---|---|
| 의사결정트리를 이용한 타이타닉 데이터셋 분석 (0) | 2020.05.19 |
| 머신러닝 연습 ① - 영화평 긍정/부정 리뷰 예측 (0) | 2020.05.14 |
| NLTK 자연어 처리 패키지 사용 (0) | 2020.05.14 |
| 베르누이 나이브베이즈 (0) | 2020.05.14 |