
하루에 하나씩 풀어보자!
1. 거듭제곱(exponentiation) 구하기
- 거듭제곱은 밑과 지수로 나타낸다.(밑 : 곱하는 수 / 지수 : 밑을 곱한 횟수)
- 예) 2가 밑이고 3이 지수인 수는 2를 3번 곱한 수로 8이다.
def exp(arg1, arg2):
x = 1
for i in range(1,arg2+1):
x *= arg1
return x
exp(3, 9)

2. 소수(prime number) 구하기
소수 : 1과 자신만을 약수로 하는 수
1) 에라토스테네스의 체
- 고대 그리스의 수학자 에라토스테네스가 만든 자연수에서 소수를 찾는 방법
- 소수가 아닌 수를 하나씩 지워내가며 찾는다.
- 공식을 사용하지 않고 소수를 구해보자.
# 약수 구하는 함수
def divisor(x):
z = []
for i in range(1,int(x/2)+1):
if x % i == 0 :
z.append(i)
z.append(x)
return z
# 소수 구하는 함수
def pn(x):
a = []
for i in range(1, x+1):
if len(divisor(i)) <= 2:
a.append(i)
return a
pn(10)

2) 페르마의 수
- 1600년대 프랑스 지방 법원에서 일했던 판사 페르마가 만든 가장 큰 소수를 찾는 방법
- n이 음이 아닌 정수일때
 형태로 나타내는 양의 정수
형태로 나타내는 양의 정수 - n이 4일때까지 소수이다.
- 페르마의 소수 공식을 사용하여 소수를 구해보자.
def fn(x) :
return(2**(2**x) + 1)
fn(4)

3) 메르센의 수

- 17세기 프랑스 수학자이자 수도사인 메르센이 만든 가장 큰 소수를 찾는 방법
- 위의 공식으로 소수를 찾는 방법
- n이 2,3,5,7,13,17,19,31,127,257 일때만 소수가 된다.
- 위의 공식을 사용하여 소수를 구해보자
def mn(x):
return (2**x)-1
mn(257)

3. 카이사르 암호
- 카이사르 암호는 기록으로 남아있는 가장 오래된 암호 중 하나이다.
- 알파벳의 순서를 n칸씩 이동시켜 만든 암호이다.
- 로마의 황제 카이사르가 브루투스에게 암살당하기 전, 친구인 키케로에게 'QHYHUWUXVWEUXWXV'
라고 적어서 보냈다. - 'QHYHUWUXVWEUXWXV'를 해석해보자!(카이사르는 알파벳을 3칸씩 이동시켰다.)
alpha = ['A','B','C','D','E','F',
'G','H','I','J','K',
'L','M','N','O','P',
'Q','R','S','T','U',
'V','W','X','Y','Z']
test = ['QHYHUWUXVWEUXWXV']
# 들어온 문장을 나누기
def cut(arg1):
a = ','.join(arg1)
a.split(',')
return a
# 문자 하나의 알파벳 위치를 파악
def alphaad(arg1):
b = cut(arg1)
c = []
for i in b:
c.append(alpha.index(i))
return c
# 입력한 숫자만큼 위치에 다하고 결과 위치의 알파벳 출력
def pw(arg1, arg2):
x = []
for i in alphaad(arg1):
i += arg2
if i < 26:
x.append(alpha[i])
else:
x.append(alpha[i-26])
y = ''
for i in x:
y += i
return y
pw(test, -3)

더 멋진 방법으로 풀어보았다!!!
아스키코드(ASCII) 사용해서 풀기
def solution(s, n) :
a = []
for i in s:
x = ord(i)
y = x + n
if (65 <= x <=90) and (65 <= y <=90):
a.append(chr(y))
elif (97 <= x <=122) and (97 <= y <=122):
a.append(chr(y))
elif (y-n) == 32:
a.append(' ')
else :
a.append(chr(y-26))
answer = ''
for i in a:
answer += i
return answer
solution('QHYHUWUXVWEUXWXV', -3)

4. 국제 표준용지
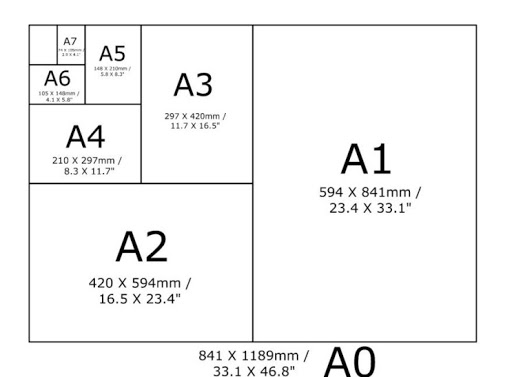
- 1919년 독일의 물리, 화학자이자 철학자인 프리드리히 오스트발트는 종이를 계속 반으로 잘라도 같은
비율을 유지하는 방법을 제안했다. - 1922년 독일공업규격 위원회는 가장 큰 종이의 넓이를 1m2으로 정하고, 가로 세로 비는 1:루트2가
되도록 종이 길이를 정했다. - A0 종이가 가로 841mm, 세로 1189mm일때, An용지의 가로, 세로 길이를 구해보자.
def An(arg1):
b = 0
a = 1189
lst = []
for i in range(1,12):
if i == 2 :
b = (round((a/2)*math.sqrt(2)))-1
lst.append([b,a])
a = b
else :
b = round((a/2)*math.sqrt(2))
lst.append([b,a])
a = b
return lst[arg1]
An(0)
An(4)
5. 공룡의 속도 구하기
- 영국의 동물학자 로버트 맥닐 알렉산더 박사는 공룡의 속도를 계산하기 위해, 공룡과 비슷한 몸매를
가진 동물들과 두발로 걷는 동물의 달리기 속도를 분석했다. - 아래의 공식을 이용하면 공룡의 속도를 구할 수 있다.
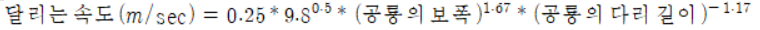
- 이 식을 이용하여 보폭이 8m, 다리 길이가 4m인 타르보사우르스의 속도를 구해보자.
def dino(arg1, arg2) :
x = 0.25*(9.8**0.5)*(arg1**1.67)*(arg2**-1.17)
print(round(x, 2),"m/sec")
dino(8, 4)

6. 삼각수
- 볼링핀처럼 어떤 물건을 일정하게 늘어놓아 삼각형으로 만들 때, 삼각형 모양을 이루는 전체 물건의
개수를 '삼각수'라고 부른다.(예 : 3, 6, 10) - 삼각수는 연속된 자연수의 합으로 나타낼 수 있다.(예 : 1+2=3, 1+2+3=6, 1+2+3+4=10)
- 삼각수 공식 :

1) 연속된 자연수 합으로 100번째 삼각수를 구하자.
def tn(arg1):
a = 0
for i in range(arg1+1):
a += i
return a
tn(100)

2) 삼각수 공식을 사용해서 100번째 삼각수를 구하자.
def tn(arg1):
a = int((arg1*(arg1+1))/2)
return a
tn(100)

3) 삼각수를 볼링핀처럼 세웠을때 몇 번이 되는지 구하자.
def x(arg1):
a = 0
for i in range(1, arg1+1):
a += i
if a == arg1 :
print(i)
x(5050)

7. 불꽃놀이와 부등식
- 불꽃은 폭죽 속에 들어 있는 화학물질의 성질에 따라 서로 다른 색을 낸다.
- 각 색깔마다 고유의 파장 영역이 달라서, 내고 싶은 색깔의 파장 영역을 활용하면 원하는 불꽃 색깔을
만들 수 있다.

def w(arg1):
if arg1 < 400:
print("보라")
elif 400 <= arg1 < 424:
print("남색")
elif 424 <= arg1 < 491:
print("파랑")
elif 491 <= arg1 < 575:
print("초록")
elif 575 <= arg1 < 585:
print("노랑")
elif 585 <= arg1 < 647:
print("주황")
elif 647 <= arg1 < 700:
print("빨강")
else:
print("700 미만의 숫자를 입력하세요.")
w(500)

+ 이미지 찾다가 발견한 신기한 사이트 :
원하는 원소를 클릭해서 불꽃놀이를 만들 수 있다.
https://javalab.org/fireworks/
참고 자료 : 수와 문자에 관한 최소한의 수학지식
https://www.aladin.co.kr/shop/wproduct.aspx?ItemId=100126522
수와 문자에 관한 최소한의 수학지식
재미있는 수학 공부를 청소년과 교양으로서의 수학을 접하는 성인을 위해 쉽고 재미있는 수학 콘텐츠를 만들어보자는 기획에서 출발하였다. 그래서 누구나 알아야 할 기본 지식을 담은 교과서에서 수학 지식을 75개...
www.aladin.co.kr
'컴퓨터 > 파이썬' 카테고리의 다른 글
| 파이썬(Python) - 날짜 / 달력 관련 라이브러리 (0) | 2020.02.25 |
|---|---|
| 파이썬(Python) - 파이썬 파일(.py) 저장 및 불러오기 (0) | 2020.02.25 |
| 파이썬(Python) - 재귀 호출 / 스택(stack) / 유클리드 호제법 (0) | 2020.02.24 |
| 파이썬(Python) - 함수 / 전역변수와 지역변수 (0) | 2020.02.22 |
| 파이썬(Python) - 조건 제어문③ for 반복문 (0) | 2020.02.20 |