
1. 텐서 생성과 변환
1) 텐서 생성
| # 라이브러리 불러오기 import numpy as np |
|
|
# 중첩 list를 지정 t = torch.tensor([[1,2],[3,4.]]) t |
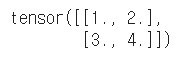 |
|
# device를 지정하면 GPU에 텐서를 만들 수 있다. t = torch.tensor([[1,2],[3,4.]],device="cuda:0") t |
 |
|
# dtype을 사용해 데이터형을 지정하여 텐서를 만들 수 있다. t = torch.tensor([[1,2],[3,4.]], dtype=torch.float64) t |
 |
|
# 0부터 9까지의 수치로 초기화된 1차원 텐서 t = torch.arange(0, 10) t |
 |
|
# 모든 값이 0인 100*10의 텐서를 작성해서 to 메서드로 GPU에 전송 t = torch.zeros(100, 10).to("cuda:0") t |
  |
|
# 정규 난수로 100*10의 텐서를 작성 t = torch.randn(100, 10) t |
 |
|
# 텐서의 shape은 size 메서드로 확인 가능 t.size() |
 |
2) 텐서 변환
|
# numpy 메서드를 사용해 ndarray로 변환 t = torch.tensor([[1,2],[3,4.]]) x = t.numpy() x |
 |
|
# GPU상의 텐서는 to 메서드로, t = torch.tensor([[1,2],[3,4.]], device="cuda:0") x = t.to("cpu").numpy() x |
 |
2. 텐서의 인덱스 조작
1) 텐서의 인덱스 조작
t = torch.tensor(([[1,2,3], [4,5,6.]]))
|
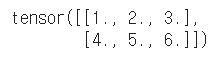 |
|
# 스칼라 첨자 지정 t[0, 2] |
 |
|
# 슬라이스로 지정 t[:, :2] |
 |
|
# 리스트로 지정 t[:, [1,2]] |
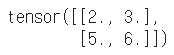 |
|
# 마스크 배열을 사용해서 3보다 큰 부분만 선택 t[t>3] |
 |
|
# [0, 1]의 요소를 100으로 설정 t[0, 1] = 100 t |
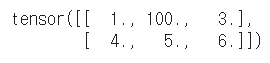 |
|
# 슬라이스를 사용한 일괄 대입 t[:, 1] = 200 t |
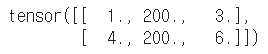 |
|
# 마스크 배열을 사용해서 특정 조건의 요소만 치환 t[t>10] = 20 t |
 |
3. 텐서 연산
1) 텐서 연산
|
# 길이 3인 벡터 v = torch.tensor([1, 2, 3.]) w = torch.tensor([0, 10, 20.]) print(v,w) |
 |
|
# 2 * 3의 행렬 m = torch.tensor([[0, 1, 2], [100, 200, 300.]]) m |
 |
|
# 벡터와 스칼라의 덧셈 v2 = v + 10 v2 |
 |
|
# 제곱도 같은 방식 v2 = v ** 2 v2 |
 |
|
# 동일 길이의 벡터 간 뺄셈 z = v - w z |
 |
|
# 여러 가지 조합 u = 2 * v - m / 10 + 6.0 u |
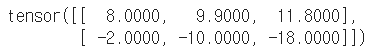 |
|
# 행렬과 스칼라 m2 = m * 2.0 m2 |
 |
|
# 행렬과 벡터 m3 = m + v m3 |
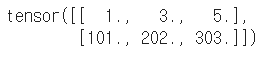 |
|
# 행렬 간 처리 m4 = m + m m4 |
 |
2) 수학 함수
|
# 100 * 10 의 테스트 데이터 생성 X = torch.randn(100, 10) X |
 |
|
# 수학 함수를 포함하는 수식 y = X * 2 + torch.abs(X) y |
 |
|
# 평균치 구하기 m = torch.mean(X) m |
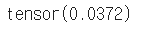 |
|
# 함수가 아닌 메서드로도 사용할 수 있다. m = X.mean() m |
 |
|
# 집계 결과는 0차원 텐서로 item 메서드를 사용해서 값을 추출할 수 있다. m_value = m.item() m_value |
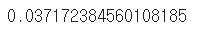 |
|
# 집계는 차원을 지정할 수도 있다. 다음은 행 방향으로 집계해서, 열 단위로 평균값을 계산한다. m2 = X.mean(0) m2 |
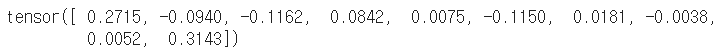 |
3) 텐서의 인덱스 조작 예
|
x1 = torch.tensor([[1, 2], [3, 4.]]) # 2*2 |
 |
|
# 2*2를 4*1로 보여 준다. x1.view(4, 1) |
 |
|
# -1은 표현할 수 있는 자동화된 값으로 대체되며, 한 번만 사용할 수 있다. x1.view(1, -1) |
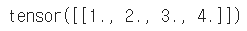 |
|
# 2*3을 전치해서 3*2로 만든다. x2.t() |
 |
|
# dim = 1로 결합하면 2*5의 텐서를 만든다. torch.cat([x1, x2], dim=1) |
 |
|
# HWC을 CHW로 변환 hwc_img_dat = torch.rand(100, 64, 32, 3) chw_img_dat = hwc_img_dat.transpose(1, 2).transpose(1, 3) print(hwc_img_dat) print(chw_img_dat) |
  |
4) 선형 대수 연산
|
m = torch.randn(100, 10) print(m) print(v) |
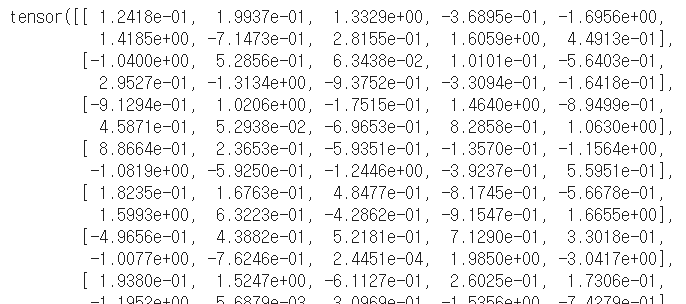  |
|
# 내적 d = torch.dot(v, v) d |
 |
|
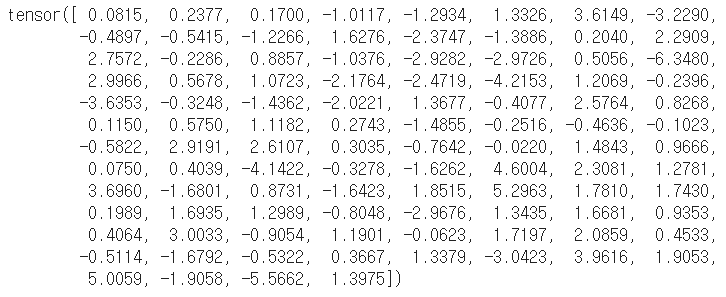
# 100 * 10의 행렬과 길이 10인 벡터의 곱 v2 = torch.mv(m, v) v2 |
 |
|
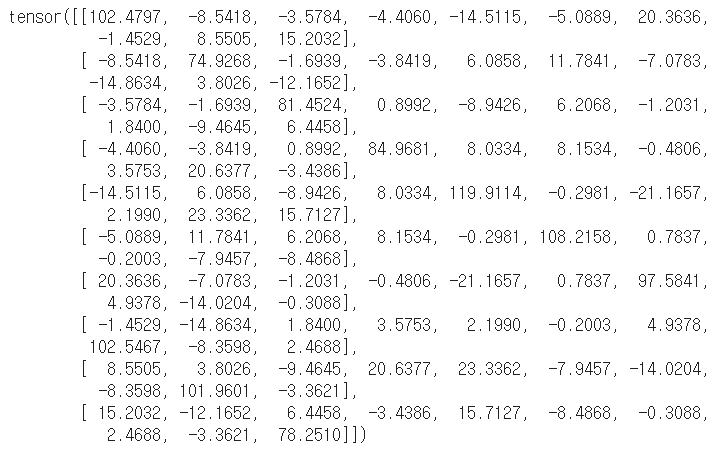
# 행렬곱 m2 = torch.mm(m.t(), m) m2 |
 |
|
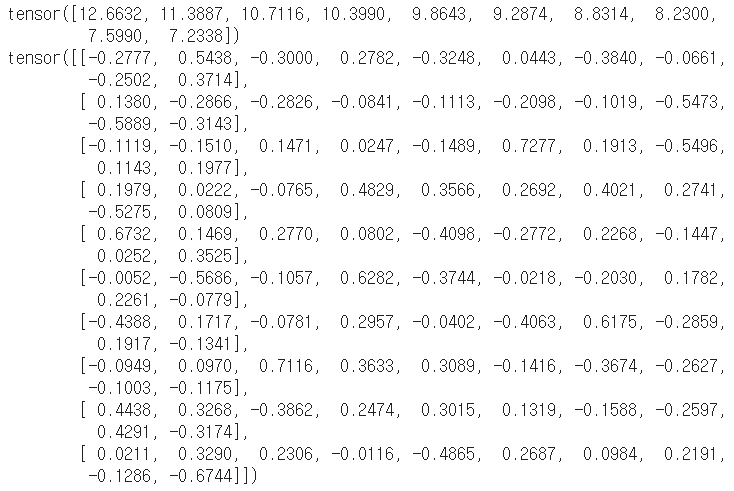
# 특이값 분해 u, s, v = torch.svd(m) print(u) print(s) print(v) |
  |
선형 대수의 연산자
| 연산자 | 설명 |
| dot | 벡터 내적 |
| mv | 행렬과 벡터의 곱 |
| mm | 행렬과 행렬의 곱 |
| matmul | 인수의 종류에 따라 자동으로 dot, mv, mm을 선택해서 실행 |
| gesv | LU 분해를 사용한 연립 방정식의 해 |
| elg, symeig | 고유값 분해, symeig는 대칭 행렬보다 효울이 좋은 알고리즘 |
| svd | 특이값 분해 |
4. 자동 미분
1) 자동 미분
|
x = torch.randn(100, 3) x |
 |
|
# 미분의 변수로 사용하는 경우는 requires_grad를 True로 설정 a = torch.tensor([1, 2, 3.], requires_grad=True) a |
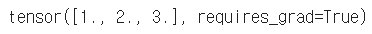 |
|
# 계산을 통해 자동으로 계산 그래프가 구축된다. y = torch.mv(x, a) o = y.sum() o |
 |
|
# 미분을 실행 o.backward() |
|
|
# 분석 답과 비교 a.grad != x.sum(0) |
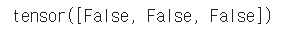 |
|
# x는 requires_grad가 False이므로 미분이 계산되지 않는다. x.grad is None |
 |
'인공지능 > 파이토치' 카테고리의 다른 글
| 파이토치 - 로지스틱 회귀 (0) | 2020.07.20 |
|---|---|
| 파이토치 - 선형 회귀 모델 (0) | 2020.07.20 |
| 파이토치 무작정 시작하기 6 - 모델 변수 프리징 (0) | 2020.07.17 |
| 파이토치 무작정 시작하기 5 - GPU를 사용한 전이 학습 (colab 사용) (0) | 2020.07.16 |
| 파이토치 무작정 시작하기 4 - CNN 기본 모델 구축 (0) | 2020.07.16 |